Gegeben sei die gebrochen rationale Funktion 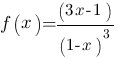
Aufgabe:
Bestimme den Definitionsbereich und finde die Nullstellen, Extrempunkte und Polstellen. Bestimme außerdem das Verhalten im Unendlichen sowie an der/den Polstelle/n.
In diesem Video zur Kurvendiskussion der Funktion f(x)=(3x-1)/(1-x)³, die du auch als Graph rechts eingezeichnet siehst, wird das Grenzwertverhalten (Randverhalten) an den Polstellen und im Unendlichen untersucht. Die komplette Kurvendiskussion dieser gebrochen rationalen Funktion findest in den weiteren Videoclips zu dieser Funktion.
Gebrochen rationale Funktionen zeichnen sich dadurch aus, dass es um Brüche geht, wobei sich im Nenner mindestens ein x befindet. Dadurch kommt es, dass es gewisse x-Werte gibt, für die die Funktion nicht definiert ist. Denn wenn im Nenner Null rauskommt, würde durch Null geteilt werden – und das geht nicht. Das ist aber noch lange nicht alles. Im Video wird auf das und vieles weitere ausführlich eingegangen.
Ein Wunschvideo für Carlos.
Viel Erfolg mit Mathehilfe24
Dein Mathehilfe24 Team
s176


Hallo Stefan,
ein sehr gutes Video, einen großen Dank schon mal dafür!
Trotzdem eine Frage, was ist eigentlich, wenn man zwei Polstellen hat, muss man sich jeweils der beiden Polstellen links und rechts nähern?
Wenn ja, wie geht man da vor?