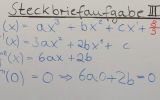Steckbriefaufgabe 6a – Funktion 3. Grades bestimmen
Im Video geht es darum, eine Funktionsgleichung 3. Grades zu finden, die bestimmten Vorgaben gerecht werden soll. Die Funktion soll dabei folgende Eigenschaften erfüllen: Sie soll einen Hochpunkt bei (1/7) und einen Tiefpunkt bei (3/1) [...] Mathe Nachhilfe online …
Trassierung – Rutsche III – Modellierung durch den Graph einer ganzrationalen Funktion
Aufgabe: Entwerfen Sie eine 4m hohe Rutsche, deren Steigung an der steilsten Stelle genau 45° beträgt.
In diesem Video wird erklärt, wie man eine ganzrationale Funktion 3. Grades anhand vorgegebener Bedindungen bestimmt (modelliert).
Ganzrationale Funktion 3. Grades bestimmen
In diesem Video wird gezeigt, wie eine ganzrationale Funktion 3. Grades bestimmt unter folgender Aufgabenstellung bestimmt wird:
Aufgabe: Die neue Umgebungsstraße soll im Punkt A (-2/1,5) “glatt” an der alten Bundesstraße anschließen, sie soll [...]
Trassierung – Rutsche II – Modellierung durch den Graph einer ganzrationalen Funktion
Das seitliche Profil der Rutsche soll durch den Graphen einer ganzrationalen Funktion modelliert werden und durch deren Extrempunkte begrenzt sein. Aufgabe: Überprüfe, ob die Rutsche den Anforderungen des TÜVs [...]
Funktionsgleichung 4. Grades bestimmen – Steckbriefaufgabe IV
Eine ganzrationale Funktion vierten Grades verläuft durch den Punkt P(-2 | -4) und besitzt im Ursprung des Koordinatensystems ein relatives Minimum. Die Steigung ihrer Tangente an der Nullstelle x = -1 beträgt 3. Aufgabe: [...]
Funktionsgleichung bestimmen II – Matrix – Gaussverfahren
Eine Parabel 4. Ordnung verläuft durch die Punkte 0(0 | 0), B(1 | -2), C(-1 | 2), D(2 | -4) und E(3 | 18). Aufgabe: Bestimmen die Gleichung der Parabel. In der Kurvendiskussion geht [...]
Funktionsgleichung aufstellen – Gaussverfahren anwenden – Parabel 3. Ordnung
Eine Parabel 3.Ordnung verläuft durch die Punkte A(0 | 2), B(1 | 3/2), C(-1 | 5/2), D(2 | 6). Aufgabe: Wie lautet die Gleichung der Parabel? Diese Aufgabe ist sozusagen das „Rückwärtsrechnen einer Kurvendiskussion“. [...]
Steckbriefaufgabe III – mit Integralrechnung
Eine Parabel 3. Ordnung hat in W( 0 / (8/9) ) einen Wendepunkt. Sie schneidet die x-Achse in N( 1 / 0 ) und begrenzt mit den Koordinatenachsen im 1. Feld eine Fläche vom Inhalt A = (15/36) FE ein.
Aufgabe: Bestimme die Funktionsgleichung.
Steckbriefaufgabe II – Ganzrationale Funktion 3. Grades bestimmen
Eine ganzrationale Funktion dritten Grades besitzt im Punkt W(2|14) eine Wendetangente mit der Steigung 15 und eine Nullstelle bei x=1. Aufgabe: Bestimme die Funktionsgleichung. In der Kurvendiskussion geht es darum, dass eine Funktionsgleichung gegeben [...]