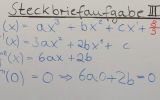Pascal´sches Dreieck – Binominalverteilung
(a + b)² = a² + 2ab + b². Das ist die zweite binomische Formel. Diese hast Du sicherlich auswendig gelernt und selbst wenn nicht – es ist sehr leicht, sie herzuleiten. Aber wie [...]
Brüche multiplizieren – Grundlagen
In diesem Video wird dir erklärt, wie Brüche zu multiplizieren sind. An sich ist die Multiplikation von Brüchen die einfachste Grundrechenart bei Brüchen. Wenn Brüche multipliziert werden, muss nicht mehr darauf geachtet werden, dass [...]
Steckbriefaufgabe III – mit Integralrechnung
Eine Parabel 3. Ordnung hat in W( 0 / (8/9) ) einen Wendepunkt. Sie schneidet die x-Achse in N( 1 / 0 ) und begrenzt mit den Koordinatenachsen im 1. Feld eine Fläche vom Inhalt A = (15/36) FE ein.
Aufgabe: Bestimme die Funktionsgleichung.
Steckbriefaufgabe II – Ganzrationale Funktion 3. Grades bestimmen
Eine ganzrationale Funktion dritten Grades besitzt im Punkt W(2|14) eine Wendetangente mit der Steigung 15 und eine Nullstelle bei x=1. Aufgabe: Bestimme die Funktionsgleichung. In der Kurvendiskussion geht es darum, dass eine Funktionsgleichung gegeben [...]
Linearfaktorzerlegung – Polynomdivision – pq Formel – Nullstellenberechnung
Gegeben ist die Funktion f(x)=-x³+4x²4x-6. Aufgabe: Zerlege in Linearfaktoren. Bei der Linearfaktorzerlegung geht es darum, ein Polynom in die linearen Faktoren zu zerlegen. Das ist klar, das hätte man sich denken [...]
Funktionsterm bestimmen – Gerade g schneidet f(x)=x³+bx²-2x+1
Inhalt des Videos
Der Graph einer Funktion f mit f(x)=x³+bx²-2x+1 schneidet die Gerade g mit der Gleichung g(x)=0,5x+2 an der Stelle x=2. Bestimme die Funktion. Wie das geht, wird in diesem Video erklärt und durchgeführt.
Nullstellen von f(x)=x³+5x²-17x-21 berechnen – Polynomdivision III
In diesem Video geht es um die Nullstellenberechnung einer kubischen Funktion. Dabei muss man die Polynomdivision anwenden, um die Gleichung lösen zu können. Weiterhin wird auch die pq-Formel angewandt, so dass dieses Video auch für das Lösen von quadratischen Gleichungen hilfreich ist.
Nullstellen der Funktion f(x)=x³-3x²-4x+12 berechnen – Polynomdivision
Gegeben ist die Funktion f(x)=x³-3x²-4x+12.
Aufgabe: Berechne die Nullstellen dieser Funktion. Wende dabei die Polynomdivision an. Bei der Polynomdivision geht es darum, dass ein Polynom (also ein Term, bei dem mindestens ein x einen höheren Exponenten als 1 besitzt) geteilt wird. In diesem Video geht es darum.
Extremwertaufgabe III – Minimale Entfernung Bär-Jäger bestimmen
Der letzte Weg des Bären Bruno wird durch die Funktion f mit der Gleichung f(x)=1/x² dargestellt.
Aufgaben: Drücken Sie die Entfernung s zwischen dem Bären und dem Schützen durch die x-Koordinate des Bären aus und berechnen Sie die Koordinaten von Brunos Schicksalsort B (xo/yo).